Korseby Online - Fraktale

Computerberechnete Fraktalbewegung

Bei noch so vielen Dingen schein es ungeklärt, doch hier ist alles anders. Unglaublich phantastisch plastische, scheinbare Bewegung von computerberechneten Fraktalgebilden, mit einer Unmenge an Farben und Formen. Wer es nicht glaubt, kann es an wenigen Zeilen Quellcode nachvollziehen..

Allgemeines

Die Programme wurden mit Turbo Pascal 6.0 für DOS geschrieben. Jedoch ist es für erfahrene Programmierer recht einfach, den Sourcecode in andere Sprachen, wie z.B. C, Java usw. zu portieren.

In der benutzten Unit MAIN.PAS, wird ein Grafikkartentreiber angesprochen (VGAVESA.BGI), der für die nötige Unterstützung der Grafikmodi sorgt. Generell kommt man aber auch mit entsprechenden Änderungen in der Unit ohne ihn aus.

Tastenbelegungen und Funktionen: Die Geschwindigkeit der Veränderung der Farben kann man mit [-] und [+] regeln. Das Programm wird mit [ESC] beendet.

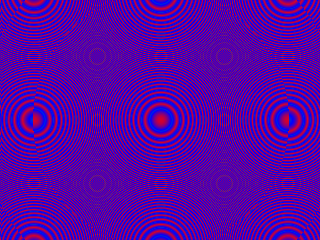
Fraktal #1

Download Fraktal #1
View Screenshot (223 KB)
Download Sourcecode (2 KB)
Download DOS-EXE (23 KB)
Das erste Fraktal liegt noch einer relativ simplen Methodik zugrunde. Mit einer einfachen Formel (in einer Iteration bzw. Schleife eingebettet) wird es berechnet:

for x:=0 to 639 do
for y:=0 to 479 do
putpixel(x,y,abs(((sqr(y-240)+sqr(x-320))shr j mod 127)-63)+16);

Für die Bewegung sorgt dann das Zusammenspiel aus 3 weiteren, relativ kleinen Prozeduren. Diese funktionieren wie folgt: Sie definieren eine simple, aus 256 Farbtönen bestehende, RGB-Farbpalette und rollen dann die einzelnen Farbeinträge nach einem bestimmten, hier definiertem, Muster.

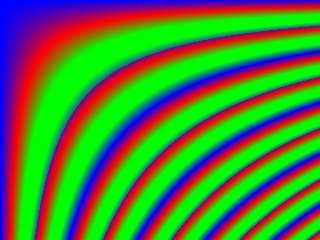
Fraktal #2

Download Fraktal #2
View Screenshot (59 KB)
Download Sourcecode (2 KB)
Download DOS-EXE (23 KB)
Das zweite Fraktal liegt nur einer Funktion zugrunde. Sie lautet folgendermaßen:

for x:=0 to 639 do
for y:=0 to 479 do
putpixel(x,y,x*y div j);

Für das Zusammenspiel, das letztendlich die Bewegung ergibt, sind, wie im obigen Fraktal, die gleichen 3 Prozeduren zuständig. Nur ergeben sie mit dieser Funktion ein völlig anderes Muster, Bild und einen Eindruck, der eine scheinbare Bewegung zeigt.

Fraktal #3

Download Fraktal #3
View Screenshot (32 KB)
Download Sourcecode (4 KB)
Download DOS-EXE (7 KB)
Das dritte Fraktal liegt nur einer einzigen Funktion zugrunde. Diesmal sind die Farbveränderungen jedoch völlig anderer Natur. Es gibt von ihnen verschiedene Funktionen (jeweils 4 an der Zahl). Somit sollte man das Fraktal nicht nur einmal aufrufen, sondern mehrmals, da das dritte Fraktal viel mehr Veränderungen und per Zufall bestimmte Prozeduren enthält, als die beiden ersten.

Die Funktion, die für die grafische Darstellung verantwortlich ist, berechnet sich folgendermaßen:

for c:=0 to 181 do
for k:=0 to 319 do
mem[$A000:k+320*(c+1)]:=round(k+c*c/60);

Es wird ersichtlich, daß in diesem Programm nicht mit den von Pascal vorgegebenen Befehlen programmiert wird, sondern über DOS-Interrupts und direktes Ansteuern der Grafikkarte. Damit wird eine gewisse Geschwindigkeitssteigerung erzielt.

Fraktal #4

Download Fraktal #4
View Screenshot 1 (123 KB)
View Screenshot 2 (17 KB)
Download Sourcecode (4 KB)
Download DOS-EXE (11 KB)
Das vierte Fraktal ist Veränderung pur. Es liegt insgesamt 16 sehr verschiedenen Funktionen zugrunde, die per Zufallsprinzip ausgewählt werden. Im Gegensatz zum 3. Fraktal wird aber nur eine Farbpalettenfunktion benutzt. Der geübte Programmierer kann aber die 3 anderen Funktionen ohne Probleme in dieses 4. Fraktal einbauen. Es scheint nur verständlich, daß die 16 Funktionen, die die einzelnen Fraktale berechnen, hier nicht aufgelistet werden können. Ein Verweis in den Quelltext Zeile 57 bis 80 ist daher angebrachter.

Auch dieses Fraktal umgeht die pascaleigenen Prozeduren und Funktionen. Es benutzt wieder die DOS-Interrupts, die speziell angesteuert werden. Für Nicht-DOS-Systeme wird die Portierung dieses Fraktals natürlich schwer werden, aber ist letztendlich nicht unmöglich.

Fraktal #5

Download Fraktal #5
View Screenshot (148 KB)
Download Sourcecode (5 KB)
Download DOS-EXE (29 KB)
Dem fünften Fraktal wurden 7 sehr eigenwillige Funktionen spendiert, die erst ab höheren Auflösungen nicht mehr pixelig aussehen. Diesmal wird zwar wieder nur eine Frabpalette benutzt, aber sie ist von den Farben her sehr unterschiedlich zu den anderen Fraktalen.
Auch diese Funktionen bestehen allesamt aus Sinus- und Cosinusberechnungen. Im Gegensatz zu den anderen Fraktalen sind sie aber etwas komplizierter. Turbo Pascal bietet zum Glück eine sehr einfache Technik, womit sich mathematische Berechnungen darstellen lassen können.

Das fünfte Fraktal benötigt keine spezielle Unit mehr. Alle Prozeduren sind im Hauptprogramm integriert. So wird die Übersichtlichkeit erhöht. Zum ersten Mal kann der Benutzer auch einen speziellen Grafikmodus wählen. Man ist nun nicht mehr nur auf 320x200 Pixel-Auflösung begrenzt, sondern kann maximal die Fraktale mit 1280x1024 Pixel berechnen lassen. Eine Auswahl findet am Anfang des Programmes statt.

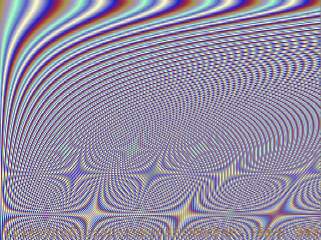
Fraktal #6

Download Fraktal #6
View Screenshot (59 KB)
Download Sourcecode (4 KB)
Download DOS-EXE (28 KB)
Auch dieses Fraktal besteht wieder aus zahlreichen Funktionen, die per Zufall ermittelt werden. Zusätzlich kann man auch zwischen verschiedenen Grafikmodi wählen. Es steht insgesamt wieder nur eine Farbpalette zur Verfügung, aber eine neue, veränderte ist ohne Probleme zu erstellen.

Die meisten Funktionen wurden diesmal mit dem Quadrat aus x bzw. y errechnet. Eine Funktion ist schon sehr kompliziert und wird mit Hilfe von arctan und pi berechnet. Auf langsamen Computern ist deshalb die Darstellung auch nicht mehr ganz so schnell, aber ab Pentium und aufwärts ist das Bild sehr fix aufgebaut.

Dieses sechste Fraktal benötigt keine Unit mehr. Alle Funktionen und Prozeduren sind im Quelltext bereits enthalten. Es kommt auch wieder der SVGA-Treiber von Borland Pascal 7.0 zum Einsatz, der ebenfalls mit dem Free Pascal Compiler angesprochen werden kann.

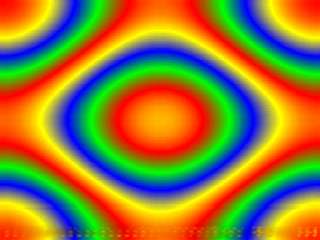
Fraktal #7

Download Fraktal #7
View Screenshot (58 KB)
Download Sourcecode (5 KB)
Download DOS-EXE (29 KB)
Das letzte der Fraktale besitzt nur 2 Funktionen zur Darstellung eines Fraktals. Der Autor fand es vor langer Zeit in einer Zeitschrift, änderte es aber grundlegend ab. So fügte Kristian Peters nicht nur die Palettenänderungsfunktionen ein, sondern machte das ganze Fraktal an sich transparent. Es verändert sich außerdem noch. Man kann nun nicht mehr nur die Geschwindigkeit der Farbpalettenänderung angeben, sondern auch die Geschwindigkeit, mit der das Fraktal sich verändern, ja gar morphen, kann.

Das Fraktal baut auf einer Sinus- bzw. Cosinusfunktion auf. Mit dieser wird das Fraktal, mit einer recht aufwendigen Farbpalette, auf den Bildschirm gezeichnet. Sie sieht folgendermaßen aus:

for x:=0 to getmaxx do f_x[x]:=trunc((sin(pi*x/160)+1)*127.5);
for x:=0 to getmaxy do f_y[x]:=trunc((sin(pi*x/100)+1)*127.5);

Zu sehen ist aber nur die Sinusfunktion. Es versteht sich übrigens fast von selbst, daß man schon schnellere Computer braucht, um die vielen Veränderungen darzustellen. Ein 386er reicht nun nicht mehr aus - Ein Pentium sollte aber genügen. Das Programm läuft zwar noch auf 386er, allerdings sehr langsam.

Auch das letzte der Fraktale benötigt keine Unit mehr. Dafür aber den SVGA-Grafikkartentreiber von Borland (ist enthalten). Man kann ebenfalls wie in den letzten Fraktalen die Grafikauflösung wählen. Aber je höher die Auflösung, desto langsamer das Fraktal.

Die Grafikunit MAIN

Download MAIN
Download Sourcecode (2 KB)
Download compiled Unit (2 KB)
Download video driver vgavesa.bgi (5 KB)
Download video driver svga256m.bgi (8 KB)
Jedes der Fraktale benötigt eine Unit, also Prozeduren und Funktionen, mit denen letztendlich das Programm gesteuert wird. Man kann diese Unit vielmehr auch als Auslagerungsdatei bezeichnen, um die Übersicht beim Programmieren zu erhalten.

Insbesondere enthält diese Unit Prozeduren für die Grafiksteuerung, also Initialisation des Grafikmodus, eine Delayroutine (weil bekanntlich die von Pascal fehlerhaft ist und nicht auf jedem Computer eine gleiche Verzögerungsrate vollbringt) und die Hauptfunktion für die Änderung der Paletteneinträge.